好的，我将严格按照您的要求，忠实地保留原文的全部内容和格式，并在每个段落后添加最长、最详细的中文解释，包括对所有公式的详细解释和举例说明。解释段落将使用自增数字的连续编号标题，并正确使用美元符号包裹公式。

十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）胶束 micelles化 micellization的热力学 Thermodynamics：一项本科生实验室实验

Juan P. Marcolongo 和 Martín Mirenda*

布宜诺斯艾利斯大学精确与自然科学学院无机、分析与物理化学 Physical Chemistry系，1428，布宜诺斯艾利斯，阿根廷

(S) 辅助信息

1. 内容解释

这个部分是文章的标题、作者信息和所属机构。

• 标题：“十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）胶束 micelles化 micellization的热力学 Thermodynamics：一项本科生实验室实验”。这个标题明确指出了文章的核心内容：研究一种叫做十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）的化学物质形成胶束 micelles过程的热力学 Thermodynamics性质，并且这篇文章是作为一个本科生可以动手操作的实验项目来介绍的。
• 作者：Juan P. Marcolongo 和 Martín Mirenda*。星号（*）通常表示通讯作者，即负责与期刊编辑和读者联系的主要研究人员。
• 所属机构：指明了作者进行研究工作的地点，即阿根廷布宜诺斯艾利斯大学的物理化学 Physical Chemistry相关院系。
• (S) 辅助信息：这是一个科学期刊文章中常见的标记，表示除了正文之外，还有一些额外的数据、实验细节或教学笔记等补充材料（Supporting Information）可以在线获取。这对于想要重复实验或深入了解细节的读者非常重要。

0 摘要

本文介绍了一项本科生实验室实验，该实验可对十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）在水溶液中形成胶束 micelles进行热力学 Thermodynamics表征。通过电导法 conductometry在不同温度下测定临界胶束 micelles浓度 Critical Micelle Concentration, CMC（CMC）和胶束 micelles电离度 degree of ionization of the micelles（ $\alpha$ ）。在简化的闭合缔合模型 closed association model框架内，该模型假设游离表面活性剂 surface active agent, surfactant单体 monomer与单分散 monodisperse胶束 micelles之间存在平衡 equilibrium，利用CMC、 $\alpha$ 及其温度依赖性计算胶束 micelles化 micellization过程的摩尔标准自由能 molar standard free energy（ $\Delta_{\text {mic }} \bar{G}$ ）、焓 enthalpy（ $\Delta_{\text {mic }} \bar{H}^{\circ}$ ）和熵 entropy（ $\Delta_{\text {mic }} \bar{S}^{\circ}$ ）。在此基础上，还对结果提出了基于表面活性剂 surface active agent, surfactant分子水合现象 hydration phenomena的物理化学 Physical Chemistry讨论。

2. 内容解释

摘要是对整篇论文的高度概括，让读者能快速了解研究的目的、方法、主要结果和结论。

• 研究目的：本文旨在提供一个适用于大学本科教学的实验方案，用于研究十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）在水中形成胶束 micelles过程的热力学 Thermodynamics特性。
• 核心物质：十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（Sodium Dodecyl Sulfate, SDS），是一种常见的阴离子 ion** anion表面活性剂 surface active agent, surfactant**，广泛用于洗涤剂、洗发水等产品中。
• 研究现象：胶束 micelles化 micellization（micellization），即表面活性剂 surface active agent, surfactant分子在溶液中浓度达到一定值后自发聚集成球状、棒状等结构的现象。
• 实验方法：电导法 conductometry（conductometry）。通过测量SDS溶液的电导率 Conductivity随浓度的变化来确定两个关键参数：
  • 临界胶束 micelles浓度 Critical Micelle Concentration, CMC**（Critical Micelle Concentration, CMC）：开始形成胶束 micelles**的最低浓度。
  • 胶束 micelles电离度 degree of ionization of the micelles**（degree of ionization of the micelles, $\alpha$）：胶束 micelles表面解离出的反离子 ion counterion数与组成胶束 micelles的表面活性剂 surface active agent, surfactant离子 ion总数之比，反映了胶束 micelles**的带电程度。
• 理论模型：“闭合缔合模型 closed association model”（closed association model）。这是一个简化的理论模型，用于描述胶束 micelles形成过程。它假设溶液中只存在两种状态的表面活性剂 surface active agent, surfactant分子：自由的单个分子（单体 monomer）和大小完全相同的胶束 micelles（单分散 monodisperse胶束 micelles），并且这两者之间处于一个动态的化学平衡 equilibrium** chemical equilibrium**中。
• 计算内容：利用实验测得的CMC和 $\alpha$ 值，以及它们如何随温度变化的规律，来计算三个核心的热力学 Thermodynamics函数：
  • 摩尔标准吉布斯自由能 molar standard Gibbs free energy**（$\Delta_{\text {mic }} \bar{G}^{\circ}$）：判断胶束 micelles化 micellization**过程能否自发进行的判据。负值表示自发。
  • 摩尔标准焓 enthalpy molar standard enthalpy**（$\Delta_{\text {mic }} \bar{H}^{\circ}$）：表示胶束 micelles化 micellization**过程中的热量变化。放热为负，吸热为正。
  • 摩尔标准熵 entropy molar standard entropy**（$\Delta_{\text {mic }} \bar{S}^{\circ}$）：表示胶束 micelles化 micellization**过程中系统混乱度的变化。熵 entropy增为正，熵 entropy减为负。
• 结果讨论：最后，文章会对计算出的热力学 Thermodynamics结果进行物理解释，特别是从“水合现象 hydration phenomena”（hydration phenomena）的角度来讨论，即水分子如何与表面活性剂 surface active agent, surfactant分子相互作用，并在胶束 micelles形成过程中发生变化。

关键词：高年级本科生，物理化学 Physical Chemistry，实验室教学，动手学习/操作，水溶液化学 Aqueous Solution Chemistry，电导率 Conductivity，胶束 micelles，有机硫化合物 Organosulfur Compounds，热力学 Thermodynamics

3. 内容解释

这部分是文章的关键词列表，用于数据库索引和文献检索，帮助其他研究人员快速找到这篇文章。

• 高年级本科生 (Upper-Division Undergraduate)：表明该实验的设计难度和深度适合大学三、四年级的学生。
• 物理化学 Physical Chemistry** (Physical Chemistry)**：指明了该实验所属的学科领域。
• 实验室教学 (Laboratory Instruction)：强调了本文的教学目的，它是一个实验指导而非纯粹的基础研究。
• 动手学习/操作 (Hands-On Learning/Manipulation)：再次突出了该实验的实践性。
• 水溶液化学 Aqueous Solution Chemistry*(Aqueous Solution Chemistry)**：说明研究的体系是在水中进行的化学过程。
• 电导率 Conductivity** (Conductivity)**：指出了核心的实验测量技术。
• 胶束 micelles** (Micelles)**：指出了研究的核心对象。
• 有机硫化合物 Organosulfur Compounds** (Organosulfur Compounds)：从化学分类上定义了SDS，因为它含有一个硫酸根基团，属于有机硫化合物 Organosulfur Compounds**。
• 热力学 Thermodynamics** (Thermodynamics)**：指出了研究的理论框架和最终目标。

1 引言

表面活性剂 surface active agent, surfactant（surface active agent）是两亲性 amphiphilic化合物，包含一个疏水“尾部” hydrophobic tail和一个极性（离子 ion或非离子 ion）“头部”。它们广泛存在于日常生活中使用的众多商业产品中，如洗涤剂、洗发水和油。尽管胶束 micelles态日益重要，但在大多数普通或实验物理化学 Physical Chemistry教科书中通常被忽视。由于这些系统对化学家来说具有明显的专业相关性，因此将其研究纳入本科教育课程是一个重要领域。

4. 内容解释

引言的第一段旨在介绍研究背景和动机。

• 定义表面活性剂 surface active agent, surfactant：首先清晰地定义了什么是表面活性剂 surface active agent, surfactant。它是一种“两亲性 amphiphilic”（amphiphilic）分子，意味着它同时具有“亲水”和“疏水”两个部分。
  • 疏水“尾部” hydrophobic tail** (hydrophobic "tail")**：通常是一条长长的碳氢链（如SDS中的十二烷基链），它不溶于水，倾向于避开水。
  • 极性“头部” (polar "head")：通常是一个离子 ion基团或强极性基团（如SDS中的硫酸根），它易溶于水，倾向于与水分子接触。
• 实际应用：强调了表面活性剂 surface active agent, surfactant的重要性，列举了它们在日常生活中的应用，如洗涤剂和洗发水，这使得研究它们具有很强的现实意义。
• 教育现状：指出了一个问题，即尽管表面活性剂 surface active agent, surfactant和胶束 micelles在工业和生活中非常重要，但在标准的物理化学 Physical Chemistry教科书中却往往被忽略。
• 研究动机：基于上述问题，作者认为将表面活性剂 surface active agent, surfactant和胶束 micelles的研究引入本科化学实验课程是非常有必要的，可以弥补课程设置上的不足，并增强学生所学知识与实际应用的联系。

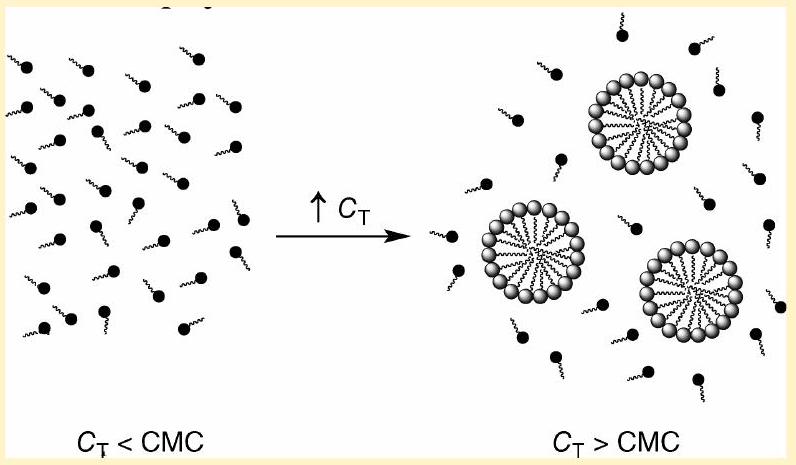
众所周知，当表面活性剂 surface active agent, surfactant浓度超过一个临界值（通常称为临界胶束 micelles浓度 Critical Micelle Concentration, CMC，CMC）时，溶液中的表面活性剂 surface active agent, surfactant分子会自发地排列成自组织 self-organized的胶束 micelles结构。本刊已提出多项实验，旨在让本科生熟悉胶束 micelles系统¹˒² 以及测定CMC值的实验技术³⁻⁷。然而，这些文章并未在本科水平上处理这些系统的热力学 Thermodynamics解释。

5. 内容解释

这一段进一步聚焦于研究的具体问题，并回顾了相关领域的已有工作（文献综述）。

• 核心概念介绍：引入了两个关键概念：
  • 临界胶束 micelles浓度 Critical Micelle Concentration, CMC** (Critical Micelle Concentration, CMC)：这是一个阈值浓度。当溶液中表面活性剂 surface active agent, surfactant的浓度低于CMC时，它们主要以单个分子的形式存在；当浓度超过CMC时，它们开始自发地聚集形成胶束 micelles**。
  • 胶束 micelles** (micelle)：这是一种自组装结构。在水溶液中，表面活性剂 surface active agent, surfactant的疏水尾部 hydrophobic tail**会聚集在一起，形成一个油性的核心，以避开水；而亲水的头部则朝向外部，与水接触，形成一个稳定的聚集体。
• 文献回顾：作者提到了在本期刊（Journal of Chemical Education）上已经发表过一些关于胶束 micelles的本科生实验。这些实验主要集中在两个方面：
  1. 让学生了解胶束 micelles系统本身。
  2. 教授学生如何用不同的实验技术（如荧光法、表面张力法等）来测量CMC值。
• 研究缺口：作者指出了现有文献的不足之处，即之前的实验虽然测量了CMC，但很少深入到对胶束 micelles形成过程进行完整的热力学 Thermodynamics解释。换句话说，它们没有系统地教学生如何从实验数据计算出吉布斯自由能、焓 enthalpy和熵 entropy，并理解这些热力学 Thermodynamics参数背后的物理意义。这正是本文要填补的空白。

在宽浓度范围内进行的离子 ion表面活性剂 surface active agent, surfactant溶液的电导率 Conductivity测量可用于确定CMC和胶束 micelles电离度 degree of ionization of the micelles $\alpha$ 。该方法依赖于溶液中游离表面活性剂 surface active agent, surfactant分子的电导率 Conductivity与胶束 micelles排列中分子相关联时的电导率 Conductivity之间的差异。尽管其应用广泛，但文献中存在不同的方法来描述观察到的电导率 Conductivity数据。一些作者认为构成胶束 micelles的表面活性剂 surface active agent, surfactant单体 monomer的电导率 Conductivity应与溶液中游离单体 monomer的电导率 Conductivity相同⁸⁻¹⁰，而另一些作者则认为该电导率 Conductivity应更方便地以斯托克斯定律 Stokes' law表示¹¹。然而，通过这两种方法获得的CMC是相同的，而 $\alpha$ 则有明显的差异。

6. 内容解释

这一段详细介绍了本研究选用的实验方法——电导法 conductometry，并指出了该方法在理论处理上存在的一些争议。

• 电导法 conductometry的原理：测量离子 ion表面活性剂 surface active agent, surfactant溶液的电导率 Conductivity可以得到CMC和胶束 micelles电离度 degree of ionization of the micelles $\alpha$。其基本原理是：
  • 在CMC以下，增加表面活性剂 surface active agent, surfactant浓度，溶液中自由移动的离子 ion（表面活性剂 surface active agent, surfactant阴离子 ion** anion和其反离子 ion counterion**，如SDS中的 S⁻ 和 Na⁺）数量成比例增加，电导率 Conductivity线性上升。
  • 在CMC以上，新加入的表面活性剂 surface active agent, surfactant分子主要形成胶束 micelles。胶束 micelles是一个体积庞大、带有部分电荷的聚集体，其移动速度远低于单个小离子 ion，并且它会束缚一部分反离子 ion** counterion**，导致溶液中有效载流子的增加速率变慢。因此，电导率 Conductivity随浓度增加的斜率 slope会突然变小。这个斜率 slope变化的转折点就是CMC。
• 理论处理上的分歧：作者指出了在分析CMC以上电导率 Conductivity数据时，文献中存在的两种不同处理方法。争议的核心在于如何估算胶束 micelles本身的电导率 Conductivity（即胶束 micelles作为一个带电粒子对总电导率 Conductivity的贡献）。
  1. 方法一：假设组成胶束 micelles的表面活性剂 surface active agent, surfactant单体 monomer在导电性上的贡献与自由单体 monomer相同。
  2. 方法二：使用斯托克斯定律 Stokes' law（Stokes' law）来估算胶束 micelles的电导率 Conductivity。斯托克斯定律 Stokes' law描述了球形物体在流体中的运动，可以关联离子 ion的尺寸、电荷和其电导能力。
• 不同方法的影响：作者强调，无论使用哪种方法，最终确定的CMC值是相同的，因为CMC是由电导率 Conductivity-浓度曲线的转折点决定的，这个点的位置不受后续斜率 slope具体模型的太大影响。但是，计算出的胶束 micelles电离度 degree of ionization of the micelles** $\alpha$ 的值会有显著差异**，因为 $\alpha$ 的计算直接依赖于CMC以上那段曲线的斜率 slope，而不同的理论模型会给出不同的斜率 slope表达式。

在不同温度下获得的CMC值可用于胶束 micelles形成的热力学 Thermodynamics表征。这需要以显式形式评估CMC的温度依赖性，这可以通过使用不同代数表达式拟合实验数据来获得。Kim和Lim¹⁶建议使用 $\ln \mathrm{CMC}=A+B T+C/T$ 形式的函数，而非广泛使用的二阶¹²˒¹⁴˒¹⁵ 和三阶多项式表达式⁹，理由是前者没有理论基础。通常，与胶束 micelles系统相关的热力学 Thermodynamics量计算不考虑 $\alpha$ 对温度的依赖性¹⁰˒¹⁷，这导致相关热力学 Thermodynamics信息存在不可忽略的差异¹⁸。

7. 内容解释

本段讨论了从实验数据到热力学 Thermodynamics参数计算过程中的关键步骤和潜在问题，即如何处理数据和选择合适的数学模型。

• 热力学 Thermodynamics表征的基础：要计算胶束 micelles化 micellization的热力学 Thermodynamics参数（如焓 enthalpy和熵 entropy），核心是需要知道CMC如何随温度变化。通过在多个不同温度下测量CMC值，可以得到一系列 (T, CMC) 数据点。
• 数据处理方法：为了从离散的数据点得到一个连续的函数关系，需要对这些数据进行拟合。文献中使用了不同的数学函数来拟合 CMC vs. T 的关系：

  • 常用方法：使用简单的多项式，如二阶（抛物线）或三阶多项式来拟合。

  • 推荐方法：Kim和Lim¹⁶ 建议使用一个更有物理背景的函数形式：

    $$\ln \mathrm{CMC}=A+B T+\frac{C}{T}$$

    其中 $A$, $B$, $C$ 是拟合常数，$T$ 是绝对温度。这种形式虽然更复杂，但被认为可能比纯粹数学上的多项式拟合更合理。

• 另一个常见问题：作者指出了一个在文献中常见的简化处理，即在计算热力学 Thermodynamics量时忽略了胶束 micelles电离度 degree of ionization of the micelles** $\alpha$ 随温度的变化**，假设它是一个常数。
• 该问题的影响：作者引用文献¹⁸指出，这种忽略 $\alpha(T)$ 依赖性的做法会导致计算出的热力学 Thermodynamics信息（特别是焓 enthalpy和熵 entropy）出现不可忽略的误差。因此，一个更精确的处理方法应该同时考虑CMC和 $\alpha$ 随温度的变化。

由于胶束 micelles系统文献中存在多种方法，以及需要在本科课程中引入新的实验室实验，本文提出了一项简单、可靠且经济的实验，用于提取离子 ion表面活性剂 surface active agent, surfactant在水溶液中胶束 micelles化 micellization过程相关的热力学 Thermodynamics信息。当前的实验室实验基于在不同温度下通过测量电导率 Conductivity来确定十二烷基硫酸钠 Sodium Dodecyl Sulfate, SDS（SDS）的CMC。使用简单的“闭合缔合模型 closed association model”，该实验涉及胶束 micelles化 micellization热力学 Thermodynamics参数的计算及其基于表面活性剂 surface active agent, surfactant分子水合现象 hydration phenomena等概念的物理解释。

8. 内容解释

这是引言的最后一段，总结了本文的目的和贡献。

• 动机总结：基于前文提到的两个问题——（1）文献中处理数据的方法不统一；（2）本科教学中缺乏此类综合性实验——作者提出了他们的解决方案。
• 本文贡献：提出一个简单、可靠且经济的本科实验方案。
  • 简单：操作不复杂，使用常规的电导率 Conductivity仪 conductivity meter即可。
  • 可靠：实验结果重现性好。
  • 经济：所用试剂和仪器成本较低。
• 实验核心内容：
  1. 在不同温度下，用电导法 conductometry测量SDS的CMC。
  2. 应用**“闭合缔合模型 closed association model”**作为理论框架。
  3. 计算全套的热力学 Thermodynamics参数（$\Delta G$, $\Delta H$, $\Delta S$）。
  4. 对结果进行深入的物理解释，特别是关联到水合现象 hydration phenomena。 这一段清晰地勾勒出了整篇文章的结构和主要内容，为读者提供了阅读路线图。

2 闭合缔合模型 closed association model

采用闭合缔合模型 closed association model来分析实验数据。该模型假设溶液中游离表面活性剂 surface active agent, surfactant分子与单分散 monodisperse胶束 micelles处于化学平衡 equilibrium** chemical equilibrium状态，每个温度下胶束 micelles均由固定数量 $n$ 的表面活性剂 surface active agent, surfactant分子组成。通常，胶束 micelles溶液并非单分散 monodisperse¹⁹˒²⁰；然而，文献中已表明²¹˒²²，这种偏差不会显著影响模型的有效性。为了描述SDS表面活性剂 surface active agent, surfactant在无盐水溶液中的胶束 micelles化 micellization过程，提出了以下平衡 equilibrium**：

$$n \mathrm{~S}^{-}+(n-m) \mathrm{Na}^{+} \stackrel{K_{\text {mic }}}{\rightleftharpoons}\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}$$

其中 $\mathrm{S}^{-}$和 $\mathrm{Na}^{+}$分别代表十二烷基硫酸根阴离子 ion** anion和钠阳离子 ion cation**，胶束 micelles $\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}$ 是带净电荷 $-m$ 的部分，包含 $n$ 个SDS分子和 $(n-m)$ 个钠离子 ion。相应的单体 monomer-胶束 micelles平衡 equilibrium常数 equilibrium constant $K_{\mathrm{mic}}$ 可表示为

$$\begin{equation*} K_{\mathrm{mic}}=\frac{\left[\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]}{\left[\mathrm{S}^{-}\right]^{n}\left[\mathrm{Na}^{+}\right]^{n-m}} \tag{1} \end{equation*}$$

其中方括号表示摩尔浓度 molar concentration。通常，CMC足够低，因此离子 ion活度系数 activity coefficient可以安全地近似为1。

9. 内容解释

这一部分详细介绍了用于分析实验数据的核心理论模型——闭合缔合模型 closed association model。

• 模型的核心假设：

  1. 二态模型：溶液中只存在两种组分：自由的表面活性剂 surface active agent, surfactant单体 monomer和胶束 micelles。不存在中间大小的聚集体。
  2. 化学平衡 equilibrium chemical equilibrium：单体 monomer和胶束 micelles之间存在一个动态的化学平衡 equilibrium** chemical equilibrium**。
  3. 单分散 monodisperse性：在特定温度下，所有胶束 micelles的大小都完全相同，都由 $n$ 个表面活性剂 surface active agent, surfactant分子构成。$n$ 被称为聚集数 aggregation number** (aggregation number)**。

• 模型的局限性与合理性：作者承认，真实的胶束 micelles溶液通常是多分散 polydisperse的，即胶束 micelles的大小存在一个分布范围，而不是单一尺寸。但作者也引用文献指出，对于热力学 Thermodynamics分析，这种简化（单分散 monodisperse假设）所带来的误差不大，不影响模型的有效性。

• 胶束 micelles化 micellization平衡 equilibrium反应式：

  $$n \mathrm{~S}^{-}+(n-m) \mathrm{Na}^{+} \stackrel{K_{\text {mic }}}{\rightleftharpoons}\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}$$

  这个化学方程式是模型的核心，描述了胶束 micelles的形成过程。* 反应物：

  • $n \mathrm{~S}^{-}$：$n$ 个十二烷基硫酸根阴离子 ion** anion**（$\mathrm{S}^{-}$），它们是表面活性剂 surface active agent, surfactant的主体。
  • $(n-m) \mathrm{Na}^{+}$：$(n-m)$ 个钠离子 ion（$\mathrm{Na}^{+}$），它们是反离子 ion** counterion**。
  • 生成物：
    • $\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}$：一个胶束 micelles。这个胶束 micelles由 $n$ 个 $\mathrm{S}^{-}$ 阴离子 ion** anion构成，但同时它也紧密地“束缚”了 $(n-m)$ 个 $\mathrm{Na}^{+}$ 阳离子 ion cation**在它的表面（称为Stern层），以部分中和其负电荷。
  • 净电荷：由于有 $n$ 个负电荷和 $(n-m)$ 个正电荷，胶束 micelles的净电荷是 $-(n - (n-m)) = -m$。所以 $m$ 代表胶束 micelles表面的有效电荷数。
  • $K_{\text {mic }}$：该平衡 equilibrium反应的平衡 equilibrium常数 equilibrium constant。

• 平衡 equilibrium常数 equilibrium constant表达式 (公式 1)：

  $$K_{\mathrm{mic}}=\frac{\left[\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]}{\left[\mathrm{S}^{-}\right]^{n}\left[\mathrm{Na}^{+}\right]^{n-m}} \tag{1}$$

  这是根据质量作用定律写出的平衡 equilibrium常数 equilibrium constant表达式。* 分子：生成物（胶束 micelles）的摩尔浓度 molar concentration $\left[\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]$。

  • 分母：反应物浓度的乘积，每种物质的浓度都取其化学计量系数作为幂。即自由 $\mathrm{S}^{-}$ 浓度的 $n$ 次方和自由 $\mathrm{Na}^{+}$ 浓度的 $(n-m)$ 次方。
  • 方括号 []：表示摩尔浓度 molar concentration（mol/L）。

• 活度系数 activity coefficient近似：作者提到，因为CMC通常很低（稀溶液），溶液中离子 ion的相互作用可以忽略不计，因此可以用浓度代替活度（即活度系数 activity coefficient $\gamma \approx 1$）。这是一个常见的简化，使得计算更加方便。

3 热力学 Thermodynamics计算

胶束 micelles形成的标准自由能 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 可以用 $K_{\mathrm{mic}}$ 表示：

$$\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ}=-R T \ln K_{\mathrm{mic}} \tag{2} \end{equation*}$$

结合方程1和2并除以 $n$，我们得到

$$\begin{align*} \frac{\Delta_{\mathrm{mic}} G^{\circ}}{n}=\Delta_{\mathrm{mic}} \bar{G}^{\circ}= & -\frac{R T}{n} \ln \left[\left(S_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]+R T \ln \left[\mathrm{~S}^{-}\right] \\ & +(1-\alpha) R T \ln \left[\mathrm{Na}^{+}\right] \tag{3} \end{align*}$$

其中 $\alpha=m/n$ 是胶束 micelles电离度 degree of ionization of the micelles。考虑到SDS胶束 micelles通常包含大量表面活性剂 surface active agent, surfactant分子（ $n>50$ ），方程3右侧的第一项相对于其他两项可以忽略不计。此外，当表面活性剂 surface active agent, surfactant浓度接近CMC时， $[\mathrm{S}^{-}] \approx [\mathrm{Na}^{+}] \approx \mathrm{CMC}$。在这种情况下，方程3可以重写为

$$\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ} \approx R T(2-\alpha) \ln \mathrm{CMC} \tag{4} \end{equation*}$$

10. 内容解释

这一部分推导了计算胶束 micelles化 micellization过程热力学 Thermodynamics参数的核心公式，起点是标准的热力学 Thermodynamics关系和闭合缔合模型 closed association model。

• 公式 (2)：吉布斯自由能与平衡 equilibrium常数 equilibrium constant的关系

  $$\Delta_{\mathrm{mic}} \bar{G}^{\circ}=-R T \ln K_{\mathrm{mic}} \tag{2}$$

  这是一个基础热力学 Thermodynamics公式，它将宏观的热力学 Thermodynamics量（标准吉布斯自由能变 $\Delta G^{\circ}$）与微观的平衡 equilibrium常数 equilibrium constant $K$ 联系起来。

  • $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$：每摩尔表面活性剂 surface active agent, surfactant单体 monomer在形成胶束 micelles过程中的标准吉布斯自由能变。上划线 $\bar{G}$ 通常表示摩尔量。
  • $R$：理想气体常数 ideal gas constant (8.314 J·K⁻¹·mol⁻¹)。
  • $T$：绝对温度 (单位：开尔文, K)。
  • $\ln K_{\mathrm{mic}}$：胶束 micelles化 micellization平衡 equilibrium常数 equilibrium constant的自然对数。 这个公式的物理意义是，平衡 equilibrium常数 equilibrium constant越大（反应越倾向于生成物），$\ln K_{\text{mic}}$ 越大，$\Delta G^{\circ}$ 就越负，表明反应的自发性越强。

• 公式 (3)：展开表达式 将公式(1)代入公式(2)，然后利用对数的性质（$\ln(a/b) = \ln a - \ln b$ 和 $\ln(x^y) = y \ln x$）进行展开，最后将总的自由能变 $\Delta_{\text{mic}} G^{\circ}$ 除以聚集数 aggregation number $n$，得到每个单体 monomer的平均自由能变 $\Delta_{\text{mic}} \bar{G}^{\circ}$。

  $$\Delta_{\mathrm{mic}} \bar{G}^{\circ} = -\frac{R T}{n} \ln \left[\left(S_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]+R T \ln \left[\mathrm{~S}^{-}\right] +(1-\alpha) R T \ln \left[\mathrm{Na}^{+}\right] \tag{3}$$

  这里引入了胶束 micelles电离度 degree of ionization of the micelles** $\alpha$** 的定义：

  $$\alpha = \frac{m}{n}$$

  它表示胶束 micelles的净电荷数 $m$ 与组成胶束 micelles的单体 monomer总数 $n$ 的比值。因此， $(n-m)/n = 1 - m/n = 1 - \alpha$。

• 简化与近似：为了得到一个更实用、能直接与实验数据联系的公式，作者做了两个关键的近似：

  1. 忽略胶束 micelles浓度项：公式(3)右边的第一项 $-\frac{R T}{n} \ln [\text{**胶束 micelles**}]$。因为 $n$ 是一个大数（对于SDS通常是50-70），所以 $1/n$ 很小。这使得第一项远小于后面两项，可以忽略。
  2. 在CMC处进行计算：CMC是胶束 micelles开始大量形成的临界点，可以近似看作是单体 monomer-胶束 micelles平衡 equilibrium发生的特征浓度。在该点，自由表面活性剂 surface active agent, surfactant阴离子 ion** anion的浓度 $[\mathrm{S}^{-}]$ 和反离子 ion counterion**浓度 $[\mathrm{Na}^{+}]$ 都约等于CMC值。
     • $[\mathrm{S}^{-}] \approx \mathrm{CMC}$
     • $[\mathrm{Na}^{+}] \approx \mathrm{CMC}$ (因为没有额外添加盐，溶液中钠离子 ion全部来自于SDS的解离)。

• 公式 (4)：最终的实用公式 将上述两个近似代入公式(3)，可以得到最终的简化表达式：

  $$\Delta_{\mathrm{mic}} \bar{G}^{\circ} \approx R T \ln (\mathrm{CMC}) + (1-\alpha) R T \ln (\mathrm{CMC}) = R T (1 + 1 - \alpha) \ln (\mathrm{CMC})$$

  $$\Delta_{\mathrm{mic}} \bar{G}^{\circ} \approx R T(2-\alpha) \ln \mathrm{CMC} \tag{4}$$

  这个公式非常重要，因为它直接将热力学 Thermodynamics量 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 与两个可以通过实验测定的物理量——CMC 和 $\alpha$——联系了起来。这样，只要在特定温度 $T$ 下测出 CMC 和 $\alpha$，就可以计算出该温度下的标准吉布斯自由能变。

上述表达式可以插入经典的吉布斯-赫姆霍兹方程 Gibbs-Helmholtz equation

$$\frac{\partial(\Delta G / T)}{\partial T}=\frac{-\Delta H}{T^{2}}$$

得到胶束 micelles形成的摩尔标准焓 enthalpy** molar standard enthalpy** $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 的以下表达式，

$$\begin{equation*} \Delta_{\mathrm{mic}} \bar{H}^{\circ} \approx-R T^{2}\left[(2-\alpha)\left(\frac{\partial \ln \mathrm{CMC}}{\partial T}\right)-\left(\frac{\partial \alpha}{\partial T}\right) \ln \mathrm{CMC}\right] \tag{5} \end{equation*}$$

最后，胶束 micelles形成的摩尔标准熵 entropy** molar standard entropy** $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 可以使用以下公式计算

$$\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ}=\Delta_{\mathrm{mic}} \bar{H}^{\circ}-T \Delta_{\mathrm{mic}} \bar{S}^{\circ} \tag{6} \end{equation*}$$

11. 内容解释

这部分接着推导了另外两个重要的热力学 Thermodynamics参数：焓 enthalpy变（$\Delta H$）和熵 entropy变（$\Delta S$）。

• 吉布斯-赫姆霍兹方程 Gibbs-Helmholtz equation

  $$\frac{\partial(\Delta G / T)}{\partial T}=\frac{-\Delta H}{T^{2}}$$

  这是一个基本的热力学 Thermodynamics关系式，它描述了吉布斯自由能 $\Delta G$ 如何随温度 $T$ 变化，并将其与焓 enthalpy变 $\Delta H$ 联系起来。这里的 $\partial / \partial T$ 表示对温度求偏导数。通过这个方程，如果我们知道了 $\Delta G(T)$ 的函数形式，就可以通过求导来得到 $\Delta H$。

• 公式 (5)：计算摩尔标准焓 enthalpy molar standard enthalpy** $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$** 推导过程如下：

  1. 将公式(4) $\Delta_{\mathrm{mic}} \bar{G}^{\circ} \approx RT(2-\alpha) \ln \mathrm{CMC}$ 两边同除以 $T$，得到 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}/T \approx R(2-\alpha) \ln \mathrm{CMC}$。
  2. 对上式两边关于温度 $T$ 求偏导。注意，这里的 $\alpha$ 和 $\mathrm{CMC}$ 都是温度的函数，所以需要使用乘法求导法则 $(uv)' = u'v + uv'$。
  3. 将求导结果代入吉布斯-赫姆霍兹方程 Gibbs-Helmholtz equation，并整理，即可得到公式(5)：

  $$\Delta_{\mathrm{mic}} \bar{H}^{\circ} \approx-R T^{2}\left[(2-\alpha)\left(\frac{\partial \ln \mathrm{CMC}}{\partial T}\right)-\left(\frac{\partial \alpha}{\partial T}\right) \ln \mathrm{CMC}\right] \tag{5}$$

  这个公式的物理意义是，胶束 micelles化 micellization的焓 enthalpy变（热效应）取决于两个因素：

  • $(\partial \ln \mathrm{CMC} / \partial T)$：CMC随温度的变化率。这可以通过对实验数据拟合出的 $\ln \mathrm{CMC}$ vs. $T$ 曲线求导数得到。
  • $(\partial \alpha / \partial T)$：胶束 micelles电离度 degree of ionization of the micelles随温度的变化率。这同样需要通过实验测量不同温度下的 $\alpha$ 值并进行拟合求导得到。 这个公式也凸显了为什么作者在引言中强调考虑 $\alpha$ 的温度依赖性是重要的。如果忽略第二项，计算出的 $\Delta H^{\circ}$ 将会不准确。

• 公式 (6)：计算摩尔标准熵 entropy molar standard entropy** $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$**

  $$\Delta_{\mathrm{mic}} \bar{G}^{\circ}=\Delta_{\mathrm{mic}} \bar{H}^{\circ}-T \Delta_{\mathrm{mic}} \bar{S}^{\circ} \tag{6}$$

  这是吉布斯自由能的定义式。一旦我们通过公式(4)计算出了 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$，并通过公式(5)计算出了 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$，就可以通过简单地重新排列这个方程来求得摩尔标准熵 entropy** molar standard entropy**变 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$：

  $$\Delta_{\mathrm{mic}} \bar{S}^{\circ} = \frac{\Delta_{\mathrm{mic}} \bar{H}^{\circ} - \Delta_{\mathrm{mic}} \bar{G}^{\circ}}{T}$$

  至此，通过测量不同温度下的CMC和 $\alpha$，我们已经建立了一套完整的方法来计算胶束 micelles化 micellization过程的三个基本热力学 Thermodynamics参数。

4 通过电导率 Conductivity测量确定CMC和 $\alpha$

胶束 micelles形成的热力学 Thermodynamics计算所需的CMC和 $\alpha$ 值可以通过电导法 conductometry获得。Bachofer previously在《本刊》中报道了离子 ion表面活性剂 surface active agent, surfactant的电导率 Conductivity测量⁴。描述离子 ion表面活性剂 surface active agent, surfactant溶液在CMC以下或以上的电导率 Conductivity的数学表达式是不同的。在CMC以下，SDS分子被认为是完全解离的1:1强电解质 strong electrolyte。在这种情况下，假设离子 ion摩尔电导率 Conductivity** ionic molar conductivity与浓度无关，表面活性剂 surface active agent, surfactant溶液的电导率 Conductivity** $\kappa$ 可以计算为

$$\begin{equation*} \kappa=\left(\lambda^{S^{-}}+\lambda^{\mathrm{Na}^{+}}\right) C_{\mathrm{T}}=p_{1} C_{\mathrm{T}} \tag{7} \end{equation*}$$

其中 $\lambda^{\mathrm{S}-}$ 和 $\lambda^{\mathrm{Na}+}$ 分别是十二烷基硫酸根阴离子 ion** anion和 $\mathrm{Na}^{+}$的离子 ion摩尔电导率 Conductivity ionic molar conductivity**（以 mS M$^{-1}$ cm$^{-1}$ 表示）， $C_{\mathrm{T}}$ 是总摩尔表面活性剂 surface active agent, surfactant浓度， $p_1$ 代表在CMC以下 $\kappa$ 对 $C_{\mathrm{T}}$ 作线性拟合的斜率 slope。

12. 内容解释

这一部分开始详细阐述如何通过电导率 Conductivity实验数据来具体确定CMC和 $\alpha$ 这两个关键参数。本段首先描述CMC以下区域的情况。

• 电导法 conductometry的基本思路：通过测量溶液电导率 Conductivity $\kappa$ 随总表面活性剂 surface active agent, surfactant浓度 $C_T$ 的变化，绘制 $\kappa$-$C_T$ 曲线。这条曲线在CMC点会有一个明显的转折（斜率 slope变化），通过分析转折前后的直线斜率 slope，就可以提取出所需信息。

• CMC以下的情况：

  • 物理图像：当浓度低于CMC时，溶液中没有胶束 micelles。SDS分子被认为是完全解离的 1:1强电解质 strong electrolyte，就像NaCl一样，在水中完全解离成 $\mathrm{S}^{-}$ 阴离子 ion** anion和 $\mathrm{Na}^{+}$ 阳离子 ion cation**。
  • 电导率 Conductivity模型：溶液的总电导率 Conductivity $\kappa$ 是所有离子 ion贡献的总和。根据科尔劳施离子 ion独立运动定律，总电导率 Conductivity约等于各离子 ion的摩尔电导率 Conductivity $\lambda$ 与其浓度的乘积之和。

• 公式 (7)：CMC以下的电导率 Conductivity

  $$\kappa=\left(\lambda^{S^{-}}+\lambda^{\mathrm{Na}^{+}}\right) C_{\mathrm{T}}=p_{1} C_{\mathrm{T}} \tag{7}$$

  • $\kappa$：溶液的电导率 Conductivity（单位：S/cm 或 mS/cm）。

  • $\lambda^{\mathrm{S}^{-}}$：十二烷基硫酸根阴离子 ion** anion的摩尔电导率 Conductivity**。

  • $\lambda^{\mathrm{Na}^{+}}$：钠离子 ion的摩尔电导率 Conductivity。

  • $C_T$：SDS的总摩尔浓度 molar concentration。因为是1:1电解质，所以 $[\mathrm{S}^{-}] = [\mathrm{Na}^{+}] = C_T$。

  • 线性关系：这个公式表明，在CMC以下，$\kappa$ 与 $C_T$ 成正比。

  • $p_1$：定义为 $\kappa$-$C_T$ 图在CMC以下区域的斜率 slope。

    $$p_1 = \lambda^{\mathrm{S}^{-}} + \lambda^{\mathrm{Na}^{+}}$$

    这个斜率 slope $p_1$ 可以通过对实验数据点进行线性拟合得到，它代表了自由的SDS单体 monomer（阴离子 ion** anion**+阳离子 ion** cation**）对电导率 Conductivity的贡献。

在CMC以上，游离SDS分子与胶束 micelles结构共存，胶束 micelles结构被认为是弱电解质 weak electrolyte。SDS浓度的增加导致胶束 micelles浓度的增加，而游离表面活性剂 surface active agent, surfactant浓度在CMC值附近实际上保持不变。在这种情况下，SDS溶液的电导率 Conductivity可以表示为

$$\begin{gather*} \kappa=\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)+\frac{C_{\mathrm{T}}-\mathrm{CMC}}{n} \lambda^{\mathrm{mic}} \\ +\left(C_{\mathrm{T}}-\mathrm{CMC}\right) \alpha \lambda^{\mathrm{Na}^{+}} \tag{8} \end{gather*}$$

其中 $\lambda^{\mathrm{mic}}$ 是胶束 micelles的离子 ion电导率 Conductivity，$(C_{\mathrm{T}}-\mathrm{CMC})/n$ 是胶束 micelles的摩尔浓度 molar concentration。原则上， $\lambda^{\mathrm{mic}}$ 的值是未知的，但可以使用两种不同的方法进行估计：（i）认为 $\lambda^{\mathrm{mic}}=n\alpha\lambda^{\mathrm{S}-}$，或（ii）采用斯托克斯定律 Stokes' law，该定律规定球形离子 ion的电导率 Conductivity与电荷的平方除以离子 ion半径成正比。使用后一种方法，获得的热力学 Thermodynamics量与文献报道的 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 值吻合良好。

13. 内容解释

本段描述了CMC以上区域的电导率 Conductivity模型，这是分析中更复杂的部分。

• CMC以上的物理图像：

  • 溶液中同时存在三种导电物质：自由的 $\mathrm{S}^{-}$ 阴离子 ion** anion**、自由的 $\mathrm{Na}^{+}$ 阳离子 ion** cation**，以及带电的胶束 micelles $(\mathrm{S}_{n} \mathrm{Na}_{n-m})^{m-}$。
  • 一个关键假设是，一旦浓度超过CMC，自由单体 monomer的浓度就基本保持在CMC值不再增加。所有新加入的SDS都用于形成胶束 micelles。
  • 胶束 micelles本身可以看作是一个“弱电解质 weak electrolyte”，因为它部分解离，释放出 $\alpha n$ 个反离子 ion** counterion**，同时自身带净电荷 $-m = -\alpha n$。

• 公式 (8)：CMC以上的电导率 Conductivity

  $$\kappa=\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)+\frac{C_{\mathrm{T}}-\mathrm{CMC}}{n} \lambda^{\mathrm{mic}} +\left(C_{\mathrm{T}}-\mathrm{CMC}\right) \alpha \lambda^{\mathrm{Na}^{+}} \tag{8}$$

  这个公式将总电导率 Conductivity $\kappa$ 分解为三个部分的贡献之和：

  1. 第一项：$\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)$ 这代表了浓度保持在CMC水平的自由单体 monomer和它们对应的反离子 ion counterion的贡献。这部分可以看作是一个恒定的背景电导率 Conductivity。
  2. 第二项：$\frac{C_{\mathrm{T}}-\mathrm{CMC}}{n} \lambda^{\mathrm{mic}}$ 这代表了胶束 micelles本身的贡献。
     • $C_T - \mathrm{CMC}$：浓度超过CMC的部分，即全部形成胶束 micelles的SDS的浓度。
     • $(C_T - \mathrm{CMC})/n$：胶束 micelles的摩尔浓度 molar concentration（因为每个胶束 micelles由 $n$ 个单体 monomer构成）。
     • $\lambda^{\mathrm{mic}}$：每个胶束 micelles的摩尔电导率 Conductivity。
  3. 第三项：$\left(C_{\mathrm{T}}-\mathrm{CMC}\right) \alpha \lambda^{\mathrm{Na}^{+}}$ 这代表了与新形成的胶束 micelles相关的额外自由反离子 ion counterion的贡献。
     • $C_T - \mathrm{CMC}$：形成胶束 micelles的SDS单体 monomer的总浓度。
     • $(C_T - \mathrm{CMC}) \alpha$：从这些胶束 micelles上解离下来的自由反离子 ion** counterion**（$\mathrm{Na}^{+}$）的总浓度。因为每个单体 monomer进入胶束 micelles后，平均会释放 $\alpha$ 个反离子 ion** counterion**。
     • $\lambda^{\mathrm{Na}^{+}}$：自由 $\mathrm{Na}^{+}$ 的摩尔电导率 Conductivity。

• 未知数 $\lambda^{\mathrm{mic}}$ 的处理： 公式(8)中有一个未知参数 $\lambda^{\mathrm{mic}}$（胶束 micelles的摩尔电导率 Conductivity）。作者提到了两种估算它的方法，并选择了第二种：

  1. 方法 (i)：假设胶束 micelles的电导率 Conductivity等于其内部所有解离的表面活性剂 surface active agent, surfactant离子 ion的电导率 Conductivity之和，即 $\lambda^{\mathrm{mic}} = n\alpha\lambda^{\mathrm{S}^{-}}$。
  2. 方法 (ii)：采用斯托克斯定律 Stokes' law。该定律认为，离子 ion的电导率 Conductivity与其（有效电荷）² 成正比，与其（水合）半径成反比。作者指出，使用这种方法得到的热力学 Thermodynamics结果与文献值吻合得更好，因此本文采用此方法。

假设胶束 micelles半径与 $n^{1/3}$ 成比例¹¹， $\lambda^{\mathrm{mic}}$ 可以近似为

$$\begin{equation*} \lambda^{\mathrm{mic}} \approx \frac{m^{2}}{n^{1/3}} \lambda^{\mathrm{S}^{-}} \tag{9} \end{equation*}$$

在斯托克斯定律 Stokes' law近似的范畴内， $\lambda^{\mathrm{mic}}$ 的值可以从 $\lambda^{\mathrm{S}-}$ 估计，即单电荷（ $m=-1$ ）SDS单体 monomer（ $n=1$ ）的电导率 Conductivity。方程8可以重新排列得到

$$\begin{equation*} \frac{\kappa-\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)}{C_{\mathrm{T}}-\mathrm{CMC}}=\frac{1}{n} \lambda^{\mathrm{mic}}+\alpha \lambda^{\mathrm{Na}^{+}} \tag{10} \end{equation*}$$

将方程7和9代入方程10并重新排列，得到以下表达式

$$\begin{equation*} \frac{\kappa-\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)}{C_{\mathrm{T}}-\mathrm{CMC}}=\frac{m^{2}}{n^{4/3}}\left(p_{1}-\lambda^{\mathrm{Na}^{+}}\right)+\alpha \lambda^{\mathrm{Na}^{+}} \tag{11} \end{equation*}$$

方程11的左侧表示CMC以上 $\kappa$ 对 $C_{\mathrm{T}}$ 作线性拟合的斜率 slope $p_2$。考虑到 $\alpha=m/n$ 的定义，此方程可以改写为二次方程

$$\begin{equation*} n^{2/3}\left(p_{1}-\lambda^{\mathrm{Na}^{+}}\right) \alpha^{2}+\lambda^{\mathrm{Na}^{+}} \alpha-p_{2}=0 \tag{12} \end{equation*}$$

14. 内容解释

这一部分是本文在数学推导上的核心，展示了如何从电导率 Conductivity数据中求解出胶束 micelles电离度 degree of ionization of the micelles $\alpha$。

• 公式 (9)：基于斯托克斯定律 Stokes' law的 $\lambda^{\text{mic}}$ 模型

  $$\lambda^{\mathrm{mic}} \approx \frac{m^{2}}{n^{1/3}} \lambda^{\mathrm{S}^{-}} \tag{9}$$

  这个公式是对斯托克斯定律 Stokes' law的具体应用。

  • 电荷：胶束 micelles的有效电荷为 $-m$，所以电导率 Conductivity正比于 $m^2$。
  • 半径：假设胶束 micelles是球形的，其体积正比于聚集数 aggregation number $n$。球的体积 $V = \frac{4}{3}\pi r^3$，所以半径 $r$ 正比于 $V^{1/3}$，即 $r \propto n^{1/3}$。电导率 Conductivity与半径成反比，所以与 $n^{1/3}$ 成反比。
  • 比例常数：$\lambda^{\mathrm{S}^{-}}$ 被用作一个参考值或比例常数，它代表了一个单体 monomer（$n=1, m=1$）的情况。

• 公式 (10)：重排公式(8) 对公式(8)进行代数变形，目的是为了分离出CMC以上区域的斜率 slope。将第一项移到左边，然后两边同除以 $(C_T - \mathrm{CMC})$，就得到了公式(10)。

  $$\frac{\kappa-\text{常数项}}{C_{\mathrm{T}}-\text{常数项}} = \text{**斜率 slope**}$$

  公式(10)的左边正是 $\kappa$ 对 $C_T$ 在CMC以上作图的斜率 slope，我们称之为 $p_2$。所以：

  $$p_2 = \frac{1}{n} \lambda^{\mathrm{mic}}+\alpha \lambda^{\mathrm{Na}^{+}}$$

• 公式 (11)：代入与替换 现在将公式(9)代入到 $p_2$ 的表达式中，并利用之前定义的 $p_1 = \lambda^{\mathrm{S}^{-}} + \lambda^{\mathrm{Na}^{+}}$（即 $\lambda^{\mathrm{S}^{-}} = p_1 - \lambda^{\mathrm{Na}^{+}}$），进行替换：

  $$p_2 = \frac{1}{n} \left( \frac{m^2}{n^{1/3}} \lambda^{\mathrm{S}^{-}} \right) + \alpha \lambda^{\mathrm{Na}^{+}} = \frac{m^2}{n^{4/3}} (p_1 - \lambda^{\mathrm{Na}^{+}}) + \alpha \lambda^{\mathrm{Na}^{+}}$$

  这就是公式(11)。

• 公式 (12)：求解 $\alpha$ 的二次方程 我们最终的目标是求 $\alpha$。在公式(11)中，我们用 $\alpha = m/n$ (即 $m = n\alpha$) 来替换 $m$：

  $$p_2 = \frac{(n\alpha)^2}{n^{4/3}} (p_1 - \lambda^{\mathrm{Na}^{+}}) + \alpha \lambda^{\mathrm{Na}^{+}} = \frac{n^2 \alpha^2}{n^{4/3}} (p_1 - \lambda^{\mathrm{Na}^{+}}) + \alpha \lambda^{\mathrm{Na}^{+}}$$

  $$p_2 = n^{2/3} \alpha^2 (p_1 - \lambda^{\mathrm{Na}^{+}}) + \alpha \lambda^{\mathrm{Na}^{+}}$$

  将上式整理成一个关于 $\alpha$ 的标准二次方程 $Ax^2 + Bx + C = 0$ 的形式，就得到了公式(12)：

  $$\underbrace{n^{2/3}\left(p_{1}-\lambda^{\mathrm{Na}^{+}}\right)}_{A} \alpha^{2}+\underbrace{\lambda^{\mathrm{Na}^{+}}}_{B} \alpha \underbrace{-p_{2}}_{C}=0 \tag{12}$$

  这个方程是求解 $\alpha$ 的关键。在这个方程中：

  • $p_1$ 和 $p_2$ 是我们可以从实验的 $\kappa$-$C_T$ 图中直接测量得到的两个斜率 slope。
  • $n$ (聚集数 aggregation number) 和 $\lambda^{\mathrm{Na}^{+}}$ (钠离子 ion摩尔电导率 Conductivity** ionic molar conductivity**) 需要从文献中查找对应温度下的值。
  • $\alpha$ 是唯一的未知数。 通过求解这个二次方程，就可以得到胶束 micelles电离度 degree of ionization of the micelles $\alpha$ 的值。

为了从方程12中评估 $\alpha$ ，需要额外的假设：

（i）首先，允许 $n$ 随温度变化。Zana及其同事¹³报告的实验数据通过内插和外推法获得了 $n$ 值： $n=72$ （ $T=284 \mathrm{~K}$ ）、 $69$ （ $T=288 \mathrm{~K}$ ）、 $65$ （ $T=293 \mathrm{~K}$ ）、 $62$ （ $T=298 \mathrm{~K}$ ）、 $59$ （ $T=303 \mathrm{~K}$ ）、 $56$ （ $T=308 \mathrm{~K}$ ）、 $54$ （ $T=313 \mathrm{~K}$ ）、 $50$ （ $T=323 \mathrm{~K}$ ）和 $47$ （ $T=333 \mathrm{~K}$ ）（见辅助信息中包含的学生书面说明）。

（ii）其次， $\lambda^{\mathrm{Na}+}$ 的值近似为无限稀释 infinite dilution溶液中的值 $\lambda_{\infty}{ }^{\mathrm{Na}+}$ 。Benson和Gordon²³报告的实验数据通过线性插值法计算了 $\lambda_{\infty}{ }^{\mathrm{Na}+}$ 值： $34.7$ （ $T=284 \mathrm{~K}$ ）、 $39.3$ （ $T=288 \mathrm{~K}$ ）、 $44.9$ （ $T=293 \mathrm{~K}$ ）、 $50.6$ （ $T=298 \mathrm{~K}$ ）、 $56.3$ （ $T=303 \mathrm{~K}$ ）、 $62.0$ （ $T=308 \mathrm{~K}$ ）、 $67.7$ （ $T=313 \mathrm{~K}$ ）、 $79.0$ （ $T=323 \mathrm{~K}$ ）和 $90.3$ （ $T=333 \mathrm{~K}$ ）（见辅助信息中包含的学生书面说明）。

15. 内容解释

这一段提供了求解公式(12)所需的两个关键参数 $n$ 和 $\lambda^{\mathrm{Na}^{+}}$ 的具体数据来源和处理方法，是理论联系实际的重要一步。

• 求解方程(12)的前提：为了解出 $\alpha$，我们需要知道方程中其他所有参数的值。其中 $p_1$ 和 $p_2$ 来自本次实验，而 $n$ 和 $\lambda^{\mathrm{Na}^{+}}$ 则需要借助外部数据。
• 假设 (i)：聚集数 aggregation number $n$ 随温度变化：
  • 作者明确指出，胶束 micelles的聚集数 aggregation number $n$ 不是一个常数，它会随着温度的改变而变化。通常情况下，对于SDS这类表面活性剂 surface active agent, surfactant，温度升高，$n$ 会减小。
  • 数据来源：作者引用了Zana等人的研究工作¹³，他们通过实验测量了不同温度下SDS胶束 micelles的聚集数 aggregation number。
  • 具体数值：这里列出了一系列在不同温度下的 $n$ 值，例如在284 K（约11°C）时 $n=72$，而在333 K（约60°C）时减小到 $n=47$。对于实验中未直接列出的温度点，可以通过插值法（在两个已知点之间估算）或外推法（在已知点范围之外估算）来获得。
• 假设 (ii)：钠离子 ion摩尔电导率 Conductivity ionic molar conductivity** $\lambda^{\mathrm{Na}^{+}}$ 的取值**：
  • 近似处理：理论上，离子 ion的摩尔电导率 Conductivity会随溶液浓度变化而略有变化。这里做了一个合理的简化：使用无限稀释 infinite dilution时的摩尔电导率 Conductivity $\lambda_{\infty}^{\mathrm{Na}^{+}}$ 来近似实际溶液中的 $\lambda^{\mathrm{Na}^{+}}$。因为实验溶液浓度总体较低，这个近似是可接受的。
  • 数据来源：作者引用了Benson和Gordon的研究²³，他们精确测量了 $\lambda_{\infty}^{\mathrm{Na}^{+}}$ 在不同温度下的值。
  • 具体数值：同样，这里列出了一系列在不同温度下的 $\lambda_{\infty}^{\mathrm{Na}^{+}}$ 值（单位应为 mS·M⁻¹·cm² 或类似单位，原文中单位可能简写），例如在298 K（25°C）时为50.6。同样，对于其他温度点，可以通过线性插值来计算。

总结：这一段的实际操作意义是，学生在做这个实验时，测量完自己数据的 $p_1$ 和 $p_2$ 后，需要查阅辅助材料或本文给出的数据表，根据自己的实验温度，通过插值找到对应的 $n$ 和 $\lambda^{\mathrm{Na}^{+}}$ 值，然后代入公式(12)，解一个一元二次方程，最终得到该温度下的胶束 micelles电离度 degree of ionization of the micelles $\alpha$。

5 材料与方法

电泳级SDS由Sigma提供并直接使用。溶液用去离子 ion水（10 MΩ cm）配制，该水先前已在配备0.22 μm孔径滤器的商用Millipore Milli-Q系统（MQ水）中过滤。为了进行电导率 Conductivity测量，配制了五种浓度低于0.20% w/v（0.01、0.05、0.09、0.12和0.18% w/v）和五种浓度高于0.30% w/v（0.30、0.40、0.50、0.60和0.70% w/v）的SDS溶液。

将装有不同浓度SDS溶液的玻璃瓶放入配有Julabo EM恒温器的恒温水槽中。温度调节精度为0.2°C。为了测定溶液的电导率 Conductivity，使用了型号为162 A的数字台式电导率 Conductivity仪 conductivity meter。该数字电导率 Conductivity仪 conductivity meter先前已用两种氯化钠标准溶液进行校准 calibration：692 ppm（1413 μS cm⁻¹）和7230 ppm（12.9 mS cm⁻¹），以确定电池常数 cell constant。

16. 内容解释

这部分详细描述了实验的具体操作流程、所用试剂和仪器，是科学论文中确保实验可重复性的关键部分。

• 试剂与溶剂：
  • SDS：使用了“电泳级”（electrophoresis grade）的SDS，这是一种高纯度等级，确保没有杂质影响电导率 Conductivity测量。供应商是Sigma公司。试剂是“直接使用”，意味着没有进行额外的纯化步骤。
  • 水：使用了高质量的去离子 ion水，电阻率高达 10 MΩ·cm，表明水中离子 ion含量极低。水还经过了0.22 μm的滤膜过滤，以去除微小颗粒和微生物。这种水通常被称为Milli-Q水或超纯水。
• 溶液配制：
  • 为了准确地确定CMC这个转折点，实验设计者在预计的CMC（约0.23% w/v）两侧都配制了一系列浓度的溶液。
  • CMC以下：配制了5个浓度点，从0.01%到0.18% w/v。
  • CMC以上：配制了5个浓度点，从0.30%到0.70% w/v。
  • 浓度单位：% w/v 表示质量/体积百分浓度，即每100毫升溶液中溶质的克数。
• 实验条件控制与测量：
  • 温度控制：将装有样品的玻璃瓶放入恒温水槽中，使用Julabo EM恒温器精确控制温度，精度为 ±0.2°C。这是进行热力学 Thermodynamics研究的基础，因为所有参数都依赖于温度。
  • 电导率 Conductivity测量：使用一台数字台式电导率 Conductivity仪 conductivity meter进行测量。
  • 仪器校准 calibration：在测量之前，用两种已知电导率 Conductivity的氯化钠（NaCl）标准溶液对电导率 Conductivity仪 conductivity meter进行了校准 calibration。校准 calibration的目的是为了精确测定电导池的“电极常数 cell constant”（cell constant），这是将仪器读数（电阻或电导）准确转换为标准电导率 Conductivity值（如 μS/cm）所必需的步骤。

6 危险性

制备SDS固体制剂溶液时必须特别小心，因为它可能引起呼吸道和皮肤过敏反应。本实验没有其他重大危险。

17. 内容解释

这一部分是关于实验安全性的说明，是任何实验指导中必不可少的内容。

• 主要危险源：固体的SDS粉末。
• 具体危害：
  • 呼吸道刺激：SDS粉末非常细小轻盈，容易被吸入，可能刺激呼吸道，引起不适或过敏反应。因此，在称量和溶解固体SDS时，应在通风橱中操作，并佩戴口罩。
  • 皮肤刺激：SDS是一种强力的去污剂，直接接触皮肤（尤其是高浓度或长时间接触）会去除皮肤表面的油脂，导致干燥、刺激或过敏。操作时应佩戴手套。
• 总体风险评估：除了处理固体SDS时需要注意外，整个实验（主要涉及稀溶液）没有其他重大的化学或物理危险。

7 结果

对SDS溶液在不同温度下进行了电导率 Conductivity测量。在标准实验室实验中获得的结果如图1所示。对于每个温度，随着SDS浓度的变化，观察到电导率 Conductivity的拐点。这些结果与Goddard和Benson观察到的结果高度一致¹⁷。

对每个温度下拐点前后的电导率 Conductivity数据进行了线性回归 linear regression分析。在所有情况下，线性拟合都是准确的，并且在所使用的浓度范围内未观察到显著的非线性偏差。CMC值通过“Williams方法”在每个温度下确定，该方法包括求解相应的线性方程组。另外，也可以采用“Phillips方法”，该方法通过一个倒高斯函数近似电导率 Conductivity-浓度曲线的二阶导数。在该方法中，CMC将与倒高斯函数的最小值重合。然而，Mosquera及其同事²⁴已表明，对于SDS，Phillips方法与Williams方法得到的结果相同。表1中所示的结果对应于Williams方法。

18. 内容解释

这部分开始呈现实验的原始数据和初步分析结果。

• 原始数据展示：
  • 实验的核心数据是不同温度下，电导率 Conductivity随SDS浓度的变化。这些数据被绘制在图1中。
  • 关键现象：如图1所示，在每个温度下，电导率 Conductivity曲线都呈现出两条斜率 slope不同的直线段，中间有一个明显的拐点（break point）。这个拐点就是临界胶束 micelles浓度 Critical Micelle Concentration, CMC**（CMC）**。
  • 结果验证：作者提到他们的实验结果与早期Goddard和Benson的经典研究¹⁷高度一致，这证明了本实验方法的可靠性。
• 数据处理与CMC的确定：
  • 线性回归 linear regression：对每个温度下的数据，将拐点前和拐点后的数据点分别进行线性回归 linear regression（linear regression），得到两条最佳拟合直线。作者提到拟合效果很好（线性度高）。
  • Williams方法：这是确定CMC的经典方法。既然我们有两条直线的方程（$y = p_1 x + b_1$ 和 $y = p_2 x + b_2$），那么这两条直线的交点的横坐标就是CMC。求解这个由两个线性方程组成的方程组，即可得到交点，从而确定CMC。
  • Phillips方法（作为对比）：作者还提到了另一种更复杂的数学方法——Phillips方法。该方法将整个曲线的转折区域看作一个平滑过渡，并通过数学手段找到“最大变化率”的点，这通常对应于曲线二阶导数的极值。
  • 方法的一致性：作者引用文献²⁴指出，对于SDS这个体系，这两种方法得到的结果是相同的。因此，他们采用了更简单直观的Williams方法（求交点）。
  • 结果呈现：通过这种方法计算出的CMC值被列在了表1中。

CMC在25°C下的值为8.2 mM，与使用相同技术获得的文献值⁵˒¹⁷˒²⁵吻合良好。不确定度 $\Delta(\mathrm{CMC})= \pm 0.1 \mathrm{~mM}$ 是通过对同一组样品进行五次独立测量取平均值计算得出的，与先前报道的值⁴相当。图2显示了 $\ln \mathrm{CMC}$ 随温度的变化，在20至25°C之间观察到一个最小值。对于SDS，不同作者通过电导法 conductometry¹⁷、声学法²⁶和紫外-可见光谱法²⁷均报道了类似最小值的存在。图2显示了采用Kim和Lim¹⁶推荐的 $\ln \mathrm{CMC}=A+B T+C/T$ 形式的拟合结果。在进行拟合时应特别注意使用绝对温度标度。通过设定 $A=-30$ 、 $B=0.0044 \mathrm{~K}^{-1}$ 和 $C=3817 \mathrm{~K}$ ，获得了 $R^2=0.9998$ 的拟合。因此，上述方程适用于计算 $\partial \ln \mathrm{CMC}/\partial T$ 。

19. 内容解释

这一段聚焦于CMC值及其随温度变化的趋势，这是进行热力学 Thermodynamics计算的关键一步。

• CMC值的验证：
  • 作者报告了在标准温度25°C（298 K）下测得的CMC值为 8.2 mM（毫摩尔/升）。
  • 他们将这个值与多个文献报道的值进行了比较，发现吻合得很好，这再次证明了实验的准确性。
  • 不确定度：通过5次重复测量，计算出CMC的测量不确定度为 ±0.1 mM，表明实验的精密度很高。
• CMC与温度的关系（图2）：
  • 图2 绘制了 $\ln(\mathrm{CMC})$ 作为纵坐标，温度 $T$ 作为横坐标的曲线。
  • 关键特征：这条曲线不是单调变化的，而是呈现出一个 U形，在20-25°C附近有一个最小值。这意味着，从低温开始升温，CMC先是减小（更容易形成胶束 micelles），达到一个最小值后，再继续升温，CMC反而会增大（更难形成胶束 micelles）。
  • 现象的普遍性：作者指出，这个U形曲线是SDS体系的典型特征，不仅通过电导法 conductometry，通过其他多种实验方法（如声学法、光谱法）也能观察到，证实了这一现象的客观存在。
• 数据拟合：
  • 为了定量描述这个U形曲线并方便求导，作者使用了引言中提到的推荐公式对实验数据点进行拟合：

    $$\ln \mathrm{CMC}=A+B T+C/T$$

  • 拟合参数：通过最小二乘法拟合，得到了最佳的参数值：$A=-30$，$B=0.0044 \mathrm{~K}^{-1}$，$C=3817 \mathrm{~K}$。
  • 拟合优度：拟合的相关系数平方 $R^2 = 0.9998$，这个值非常接近1，表明该函数形式能够非常好地描述实验数据。
  • 应用：有了这个精确的拟合方程，就可以通过解析求导来计算任意温度下的导数 $\partial \ln \mathrm{CMC}/\partial T$，这是计算焓 enthalpy变 $\Delta H^{\circ}$ 所必需的。

    $$\frac{\partial \ln \mathrm{CMC}}{\partial T} = B - \frac{C}{T^2}$$

在每个温度下， $\alpha$ 通过方程12计算。在整个温度范围内，观察到 $\alpha$ 随温度呈线性依赖关系，斜率 slope为 $0.0013 \mathrm{~K}^{-1}$ （数据未显示）。此时，CMC、 $\alpha$ 及其温度依赖性可直接用于分别使用方程5和6计算 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 。在不同温度下获得的 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 、 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 结果列于表1中，并描绘在图3中。请注意， $\Delta_{\mathrm{mic}} \bar{G}^{\circ}(T=298 \mathrm{~K})=-21.2 \mathrm{~kJ} \mathrm{~mol}^{-1}$ 的值与Benrraou等人¹³获得的值相同，也接近Aniansson等人¹⁹报道的值（ $-22.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$ ）。 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 值略低于文献中发现的量热值 calorimetric values¹⁴˒²⁸。有趣的是， $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 在所有温度下保持负值且相对恒定，证实当浓度达到CMC值时，胶束 micelles形成是自发发生的。此外， $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 值的恒定性揭示了在所有温度下 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $T\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 之间的抵消效应。

20. 内容解释

这一段报告了 $\alpha$ 的计算结果以及最终的热力学 Thermodynamics参数计算结果，并对这些结果进行了初步分析。

• $\alpha$ 的计算与趋势：
  • 在每个实验温度下，利用之前测得的斜率 slope $p_1$ 和 $p_2$，以及从文献查得的 $n$ 和 $\lambda^{\mathrm{Na}^{+}}$，代入方程(12)，解出胶束 micelles电离度 degree of ionization of the micelles $\alpha$。
  • 温度依赖性：将不同温度下的 $\alpha$ 值作图（文中说数据未显示），发现 $\alpha$ 随温度线性增加，斜率 slope为 0.0013 K⁻¹。这意味着温度越高，胶束 micelles表面的反离子 ion** counterion**解离得越多，胶束 micelles的有效电荷也越大。这个线性关系可以用来计算导数 $\partial \alpha / \partial T$。
• 热力学 Thermodynamics参数的计算：
  • 现在，所有计算所需的要素都已备齐：CMC(T)、$\alpha(T)$，以及它们的温度导数。
  • 将这些值代入公式(4)、(5)、(6)，就可以计算出在每个温度下的 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$、$\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$。
• 结果展示与验证：
  • 所有计算结果汇总在表1中，并绘制在图3中。
  • $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 的验证：在25°C时计算出的值为 -21.2 kJ/mol。这个值与其他文献报道的值非常接近，验证了整个实验和计算方法的准确性。
  • $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 的比较：作者坦诚，他们通过吉布斯-赫姆霍兹方程 Gibbs-Helmholtz equation（一种间接方法）计算出的焓 enthalpy变值，比用量热法（直接测量热量变化）得到的值要略低一些。这可能是由于模型简化或数据处理中的微小误差造成的。
• 对热力学 Thermodynamics结果的初步观察（图3）：
  • 自发性：在所有研究的温度范围内，$\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 始终为负值，这表明胶束 micelles的形成是一个自发过程。
  • $\Delta G^{\circ}$ 的恒定性：$\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 的值随温度变化很小，几乎是一条平线。
  • 焓 enthalpy熵 entropy补偿：由于 $\Delta G^{\circ} = \Delta H^{\circ} - T\Delta S^{\circ}$，而 $\Delta G^{\circ}$ 几乎不变，这必然意味着 $\Delta H^{\circ}$ 和 $T\Delta S^{\circ}$ 这两项在很大程度上相互抵消了它们随温度的变化。从图3可以看出，$\Delta H^{\circ}$ 和 $T\Delta S^{\circ}$ 都随温度有显著的线性变化，但它们的差值却保持稳定。这种现象被称为焓 enthalpy-熵 entropy补偿效应 enthalpy-entropy compensation** (enthalpy-entropy compensation)**。

表1. 不同温度下SDS胶束 micelles化 micellization的CMC、 $\alpha$ 和热力学 Thermodynamics参数

T/K	CMC/mM	$\alpha$	$\Delta_{\mathrm{mic}} \bar{G}^{\circ} /\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$	$\Delta_{\mathrm{mic}} \bar{H}^{\circ} /\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$	$\Delta_{\mathrm{mic}} \bar{S}^{\circ} /\left(\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\right)$
284	8.4	0.19	-20.4	-0.6	70
288	8.2	0.20	-20.7	-2.1	65
293	8.0	0.21	-21.1	-4.1	58
298	8.2	0.22	-21.2	-6.2	50
303	8.2	0.22	-21.6	-8.3	44
308	8.4	0.23	-21.7	-10.3	37
313	8.7	0.24	-21.8	-12.5	30
323	9.2	0.25	-22.1	-16.7	17
333	9.2	0.26	-22.3	-21.0	4

21. 内容解释

这张表格是本文核心数据的汇总，直观地展示了实验测量值和最终计算出的热力学 Thermodynamics参数随温度的变化情况。

• 第一列 (T/K)：实验进行的绝对温度，单位是开尔文（K）。
• 第二列 (CMC/mM)：在对应温度下，通过电导法 conductometry测得的临界胶束 micelles浓度 Critical Micelle Concentration, CMC，单位是毫摩尔/升（mM）。我们可以看到，CMC值先减小后增大，在293 K到303 K之间达到最小值，这与图2的U形曲线一致。
• 第三列 ($\alpha$)：在对应温度下，通过公式(12)计算出的胶束 micelles电离度 degree of ionization of the micelles。可以看到，$\alpha$ 随温度的升高而单调增加，从0.19增加到0.26。
• 第四列 ($\Delta_{\mathrm{mic}} \bar{G}^{\circ}$)：计算出的摩尔标准吉布斯自由能 molar standard Gibbs free energy变，单位是千焦/摩尔（kJ/mol）。这些值全部为负，且变化范围很小（从-20.4到-22.3），印证了胶束 micelles化 micellization是自发过程且 $\Delta G^{\circ}$ 相对恒定。
• 第五列 ($\Delta_{\mathrm{mic}} \bar{H}^{\circ}$)：计算出的摩尔标准焓 enthalpy molar standard enthalpy变，单位是千焦/摩尔（kJ/mol）。焓 enthalpy变随温度升高而变得越来越负（放热越来越多）。在低温区（284 K），焓 enthalpy变接近于零，甚至可能为正（吸热），而在高温区则变为显著的放热过程。
• 第六列 ($\Delta_{\mathrm{mic}} \bar{S}^{\circ}$)：计算出的摩尔标准熵 entropy molar standard entropy变，单位是焦耳/(开尔文·摩尔)（J·K⁻¹·mol⁻¹）。熵 entropy变随温度升高而显著减小，从低温下较大的正值（70 J·K⁻¹·mol⁻¹）减小到高温下很小的正值（4 J·K⁻¹·mol⁻¹）。

表格总结：这张表格清晰地展示了SDS胶束 micelles化 micellization过程的热力学 Thermodynamics全貌。它不仅给出了最终的热力学 Thermodynamics函数值，还保留了中间的关键实验数据（CMC和$\alpha$），让读者可以清楚地看到从实验到结论的整个逻辑链条。这些数据是后续进行物理化学 Physical Chemistry讨论的基础。

图1. 在11°C (•)、15°C (◊)、20°C (△)、25°C (▲)、30°C (●)、35°C (○)、40°C (□)、50°C (■) 和60°C (×) 下记录的电导率 Conductivity ( $\kappa$ ) 随SDS浓度的变化。

22. 内容解释

这张图是本文最原始的实验数据图，展示了电导法 conductometry测定CMC的原理和结果。

• 坐标轴：
  • 横坐标 (SDS concentration / % w/v)：SDS的浓度，单位是质量/体积百分比。
  • 纵坐标 (Conductivity, $\kappa$ / mS cm⁻¹)：溶液的电导率 Conductivity，单位是毫西门子/厘米。
• 数据系列：图中的每条线（用不同符号表示）代表在一个特定温度下测得的一系列数据点。例如，黑三角(▲)代表25°C下的数据。
• 图像特征：
  • 两段线性区：对于每条温度曲线，都可以清晰地看到它由两段近似直线的部分组成。
  • 斜率 slope变化：在低浓度区，直线的斜率 slope较大；在高浓度区，直线的斜率 slope明显变小。
  • 拐点 (Kink)：两条直线的转折点非常明显。这个拐点在横坐标上对应的浓度值，就是该温度下的临界胶束 micelles浓度 Critical Micelle Concentration, CMC（CMC）。
• 物理意义：
  • 斜率 slope**$p_1$（低浓度区）：反映了自由的SDS单体 monomer**（$\mathrm{S}^{-}$ 和 $\mathrm{Na}^{+}$ 离子 ion）对电导率 Conductivity的贡献。浓度每增加一个单位，就相应增加了一定数量的自由离子 ion，电导率 Conductivity因此快速上升。
  • 斜率 slope**$p_2$（高浓度区）：反映了新加入的SDS形成胶束 micelles后对电导率 Conductivity的贡献。由于胶束 micelles体积大、移动慢，并且会束缚部分反离子 ion counterion**，导致电导率 Conductivity的增加速率远低于低浓度区。
• 温度效应：从图中可以看出，温度对电导率 Conductivity有显著影响。在相同浓度下，温度越高，离子 ion的运动速度越快，溶液的电导率 Conductivity也越高。因此，整个曲线族随着温度的升高而向上平移。

图2. SDS的 $\ln \mathrm{CMC}$ 随温度的变化。实线表示 $\ln \mathrm{CMC}=A+B T+C/T$ 形式的函数。误差棒是根据对同一组样品进行五次独立测量取平均值计算得出的。

23. 内容解释

这张图展示了从图1中提取出的CMC值是如何随温度变化的，是进行热力学 Thermodynamics分析的关键中间步骤。

• 坐标轴：
  • 横坐标 (Temperature / K)：绝对温度，单位是开尔文。
  • 纵坐标 ($\ln \mathrm{CMC}$)：临界胶束 micelles浓度 Critical Micelle Concentration, CMC的自然对数。取对数是为了与热力学 Thermodynamics公式（如公式4）的形式保持一致，并且通常能使数据呈现出更好的规律性。
• 数据点与误差棒：
  • 图中的每个点代表在一个特定温度下测得的 $\ln(\mathrm{CMC})$ 值。
  • 每个点上的误差棒 (error bars) 显示了该测量值的不确定度范围，这是通过多次重复实验计算得到的，反映了实验结果的精密度。
• 曲线特征：
  • 数据点清晰地呈现出一个 U形（或抛物线形） 的趋势，在约295 K（22°C）附近达到一个最小值。
• 拟合曲线（实线）：
  • 图中的实线是对这些实验数据点进行数学拟合后得到的曲线。
  • 使用的拟合函数是 $\ln \mathrm{CMC}=A+B T+C/T$。
  • 从图中可以看出，这条实线非常好地穿过了所有数据点的中心，表明该函数能够精确地描述CMC随温度变化的复杂行为。
• 图像的意义：
  1. 直观展示：直观地显示了SDS胶束 micelles化 micellization行为对温度的敏感性，并揭示了其非单调的变化规律。
  2. 定量分析的基础：这条拟合曲线的数学表达式是后续计算热力学 Thermodynamics参数（特别是焓 enthalpy变 $\Delta H^{\circ}$）的直接依据，因为我们需要对它求导数 $\partial(\ln \mathrm{CMC})/\partial T$。

图3. 热力学 Thermodynamics参数 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 、 $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $T\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 随温度的变化。

24. 内容解释

这张图是本文最重要的结果图，它将最终计算出的三个核心热力学 Thermodynamics参数随温度的变化关系可视化地呈现出来。

• 坐标轴：
  • 横坐标 (Temperature / K)：绝对温度，单位是开尔文。
  • 纵坐标 (Thermodynamic parameters / kJ mol⁻¹)：热力学 Thermodynamics参数的值，单位是千焦/摩尔。
• 三条曲线：
  1. $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ (吉布斯自由能变，通常用方块等符号表示)：
     • 这条线几乎是水平的，且全部位于零点以下（负值）。
     • 物理意义：$\Delta G^{\circ} < 0$ 表明SDS的胶束 micelles化 micellization在整个研究温度范围内都是一个自发过程。其值随温度变化很小，说明过程的自发性强度对温度不敏感。
  2. $\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ (焓 enthalpy变，通常用圆圈等符号表示)：
     • 这条线是一条斜率 slope很陡的直线，随温度升高而急剧下降。
     • 物理意义：在低温区（< 285 K），$\Delta H^{\circ}$ 接近零或为正值，说明此时胶束 micelles化 micellization过程是吸热的或不放热。随着温度升高，$\Delta H^{\circ}$ 变为负值且越来越负，说明过程转变为放热的，并且放热效应越来越强。
  3. $T\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ (熵 entropy变贡献项，通常用三角等符号表示)：
     • 这条线也是一条斜率 slope很陡的直线，同样随温度升高而急剧下降。
     • 物理意义：由于 $\Delta S^{\circ}$ 本身是正值（见表1），所以 $T\Delta S^{\circ}$ 代表了熵 entropy对吉布斯自由能的贡献（$-\Delta G = -(\Delta H - T\Delta S)$）。在低温区，$T\Delta S^{\circ}$ 是一个大的正值，是驱动反应自发进行的主要因素。随着温度升高，$T\Delta S^{\circ}$ 逐渐减小，熵 entropy的驱动作用减弱。
• 焓 enthalpy**-熵 entropy补偿现象**： 这张图是焓 enthalpy**-熵 entropy补偿的经典展示。$\Delta H^{\circ}$ 和 $T\Delta S^{\circ}$ 两条线几乎是平行的，它们都随温度发生剧烈变化，但它们的差值** $\Delta H^{\circ} - T\Delta S^{\circ}$（即 $\Delta G^{\circ}$）却几乎保持不变。这说明焓 enthalpy变和熵 entropy变的变化是协同的、相互补偿的。

8 讨论

从这些实验中获得的热力学 Thermodynamics信息可能有助于激发学生对原始数据进行批判性评估的兴趣。在这种背景下，实验室教师可能会提出几个相关问题：

• 为什么在室温下，尽管表面活性剂 surface active agent, surfactant在组织成胶束 micelles实体时采取了更有序的构型，但 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 仍然是正的？
• 为什么随着温度升高， $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 会下降？
• 胶束 micelles化 micellization过程是焓 enthalpy驱动过程 enthalpy-driven process还是熵 entropy驱动过程 entropy-driven process？

25. 内容解释

这部分是论文的讨论部分，旨在对实验结果进行深入的物理解释，并将其作为教学工具，引导学生进行思考。

• 教学目的：作者明确指出，本节的目的是利用实验获得的热力学 Thermodynamics数据，激发学生进行批判性思维。不仅仅是接受数据，而是要理解数据背后的物理化学 Physical Chemistry原理。
• 引导性问题：为了达到这个目的，作者（作为“实验室教师”的角色）提出了三个核心问题。这三个问题层层递进，直指胶束 micelles化 micellization热力学 Thermodynamics的本质。
  1. 问题一：熵 entropy增的悖论
     • 表面现象：许多单个、自由运动的表面活性剂 surface active agent, surfactant分子聚集成一个结构规整的胶束 micelles，从表面活性剂 surface active agent, surfactant分子的角度看，这是一个从无序到有序的过程，熵 entropy应该是减少的（$\Delta S < 0$）。
     • 实验事实：然而，实验结果（表1）显示，在室温下 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 是一个大的正值。
     • 核心矛盾：这个明显的矛盾需要一个更深层次的解释。
  2. 问题二：熵 entropy变随温度的变化
     • 实验事实：表1显示，$\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 随着温度的升高而减小。
     • 需要解释：为什么熵 entropy增的效应会随着温度升高而减弱？
  3. 问题三：过程的驱动力
     • 热力学 Thermodynamics驱动力：一个自发过程（$\Delta G < 0$）可以由焓 enthalpy驱动（$\Delta H < 0$，放热）、熵 entropy驱动（$\Delta S > 0$，熵 entropy增），或两者共同驱动。
     • 需要判断：根据图3和表1的数据，SDS的胶束 micelles化 micellization过程，其主要驱动力是什么？这个驱动力是否随温度而改变？

这些问题为接下来的段落设定了讨论的框架，使得解释更有针对性。

作为对这些问题的可能回答，可以考虑以下物理论点。与溶液中的单体 monomer状状态相比，聚集成胶束 micelles状态的表面活性剂 surface active agent, surfactant表现出更有序的结构。因此，人们可能会倾向于得出胶束 micelles化 micellization应该涉及系统熵 entropy减少的结论。然而，这种推理与实验证据不符，实验证据表明在低温下 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 为正。这种表面上的悖论可以通过考虑仅凭表面活性剂 surface active agent, surfactant的自由度 degrees of freedom不能提供完整图像，并且表面活性剂 surface active agent, surfactant结构的重组涉及伴随的溶剂结构变化来解释。事实上，围绕胶束 micelles的水分子与溶剂化单个SDS单体 monomer的水分子相比，其组织程度较低。这种效应会导致一个正的熵 entropy贡献，该贡献超过了由于SDS自由度 degrees of freedom损失而引起的熵 entropy减少。

26. 内容解释

这一段详细解答了第一个问题，即为什么胶束 micelles化 micellization过程的熵 entropy变是正的，引入了著名的疏水效应 hydrophobic effect** (hydrophobic effect)**。

• 分析系统总熵 entropy变：要理解总熵 entropy变 $\Delta S^{\circ}$，不能只看溶质（表面活性剂 surface active agent, surfactant），还必须考虑溶剂（水）的变化。总熵 entropy变是这两部分变化之和：

  $$\Delta S_{\text{总}} = \Delta S_{\text{**表面活性剂 surface active agent, surfactant**}} + \Delta S_{\text{水}}$$

• 表面活性剂 surface active agent, surfactant的熵 entropy变 ($\Delta S_{\text{**表面活性剂 surface active agent, surfactant**}}$)：
  • 当自由的、可以随意平动和转动的单个表面活性剂 surface active agent, surfactant分子被束缚进一个胶束 micelles结构中时，它们的运动自由度 degrees of freedom大大降低。
  • 这是一个从无序到有序的过程。
  • 因此，这部分的熵 entropy变是负的 ($\Delta S_{\text{**表面活性剂 surface active agent, surfactant**}} < 0$)。
• 水的熵 entropy变 ($\Delta S_{\text{水}}$)：
  • 这是理解悖论的关键。当单个表面活性剂 surface active agent, surfactant分子的疏水尾部 hydrophobic tail（碳氢长链）分散在水中时，为了最大限度地维持水分子之间的氢键网络，水分子会在疏水尾部 hydrophobic tail周围形成一个高度有序的、类似“笼子”或“冰山”的结构。这种结构比普通液态水更有序。
  • 当胶束 micelles形成时，所有疏水尾部 hydrophobic tail都聚集到了胶束 micelles内部，不再与水直接接触。
  • 这导致原本束缚在疏水尾部 hydrophobic tail周围的那些高度有序的水分子被释放出来，回归到无序的、自由的本体水中。
  • 这是一个从有序到无序的过程。
  • 因此，这部分的熵 entropy变是大的正值 ($\Delta S_{\text{水}} > 0$)。
• 结论：
  • 胶束 micelles化 micellization过程的总熵 entropy变是表面活性剂 surface active agent, surfactant熵 entropy减和水分子熵 entropy增共同作用的结果。
  • 实验观察到 $\Delta_{\mathrm{mic}} \bar{S}^{\circ} > 0$，这表明水分子被释放所带来的巨大熵 entropy增，超过了表面活性剂 surface active agent, surfactant分子聚集所造成的熵 entropy减。
  • 因此，胶束 micelles化 micellization的主要熵 entropy驱动力来自于溶剂（水），而不是溶质本身。这个现象就是“疏水效应 hydrophobic effect”的核心。

随着温度升高，表面活性剂 surface active agent, surfactant分子的溶剂化结构预计会逐渐减弱。Evans和Wightman¹⁸表明，对于十四烷基三甲基溴化铵，溶剂化效应在高于116°C的温度下变得可以忽略不计。因此，当温度升高时，由于水分子在胶束 micelles化 micellization过程中的贡献减少，预计 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 会下降。

27. 内容解释

这一段解答了第二个问题：为什么 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 会随着温度的升高而下降。

• 温度对水结构的影响：
  • 在低温下，水分子之间的氢键网络比较强，疏水尾部 hydrophobic tail周围形成的“笼状”水结构也比较稳定和有序。
  • 随着温度的升高，分子的热运动加剧，水分子自身的氢键网络已经被部分破坏，整体结构变得更加无序。
  • 因此，在高温下，疏水尾部 hydrophobic tail周围的溶剂化水层本身就没有那么有序了。
• 对熵 entropy变的贡献：
  • 低温时：胶束 micelles化 micellization过程释放的是高度有序的水分子，使其变为无序的本体水，熵 entropy的增加量（$\Delta S_{\text{水}}$）非常大。
  • 高温时：胶束 micelles化 micellization过程释放的是本身就不太有序的水分子，使其变为无序的本体水，熵 entropy的增加量（$\Delta S_{\text{水}}$）就相对较小。
• 结论：
  • 因为胶束 micelles化 micellization的总正熵 entropy变主要来自于水分子的贡献，而这个贡献随着温度的升高而减小，所以总的 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 就会随温度升高而下降。
  • 作者还引用了一个极端例子：对于另一种表面活性剂 surface active agent, surfactant，当温度足够高（>116°C）时，水的溶剂化效应几乎消失，届时熵 entropy变可能就不再是主要驱动力了。

$\Delta_{\mathrm{mic}} \bar{H}^{\circ}$ 和 $\Delta_{\mathrm{mic}} \bar{S}^{\circ}$ 随温度显示出大的线性变化。然而，这些变化相互抵消，导致 $\Delta_{\mathrm{mic}} \bar{G}^{\circ}$ 的值在整个研究温度范围内几乎不变。这种现象在文献中被称为“补偿现象”。从这个热力学 Thermodynamics观点来看，SDS胶束 micelles化 micellization在低温下被认为是熵 entropy驱动过程 entropy-driven process，在高温下被认为是焓 enthalpy驱动过程 enthalpy-driven process。

28. 内容解释

这一段解答了第三个问题，即胶束 micelles化 micellization过程的驱动力是什么，并总结了焓 enthalpy-熵 entropy补偿现象。

• 回顾焓 enthalpy**-熵 entropy补偿**：
  • 如图3所示，$\Delta H^{\circ}$ 和 $\Delta S^{\circ}$（或 $T\Delta S^{\circ}$）都对温度非常敏感，呈线性变化。
  • 但它们的变化方式恰好使得它们的组合 $\Delta G^{\circ} = \Delta H^{\circ} - T\Delta S^{\circ}$ 几乎不随温度变化。
• 过程驱动力的转变：
  • 在低温区（例如 284 K）：
    • $\Delta H^{\circ} \approx -0.6 \mathrm{~kJ/mol}$ (接近于零，对自发性贡献很小)。
    • $-T\Delta S^{\circ} = -284 \mathrm{K} \times 70 \mathrm{~J K^{-1} mol^{-1}} = -19.88 \mathrm{~kJ/mol}$ (一个大的负值)。
    • 此时，$\Delta G^{\circ}$ 的负值几乎完全由熵 entropy项 $T\Delta S^{\circ}$ 贡献。因此，在低温下，胶束 micelles化 micellization是一个典型的熵 entropy驱动过程 entropy-driven process** (entropy-driven process)。其根本原因是疏水效应 hydrophobic effect**。
  • 在高温区（例如 333 K）：
    • $\Delta H^{\circ} \approx -21.0 \mathrm{~kJ/mol}$ (一个大的负值，强烈的放热)。
    • $-T\Delta S^{\circ} = -333 \mathrm{K} \times 4 \mathrm{~J K^{-1} mol^{-1}} = -1.33 \mathrm{~kJ/mol}$ (贡献已经变得很小)。
    • 此时，$\Delta G^{\circ}$ 的负值主要来自于焓 enthalpy项 $\Delta H^{\circ}$ 的贡献。因此，在高温下，过程转变为焓 enthalpy驱动过程 enthalpy-driven process** (enthalpy-driven process)**。
    • 焓 enthalpy变为负的原因可能与胶束 micelles核心形成时，碳氢链之间的范德华吸引力有关。
• 总结：SDS胶束 micelles化 micellization的驱动力不是一成不变的。它经历了一个从低温下的熵 entropy驱动到高温下的焓 enthalpy驱动的平滑过渡。这个有趣的转变是理解胶束 micelles化 micellization热力学 Thermodynamics全貌的关键。

9 结论

我们提出了一项新的实验室实验，通过胶束 micelles系统引入基本热力学 Thermodynamics概念。数据的合理化可以置于“闭合缔合模型 closed association model”的框架内，该模型建立了表面活性剂 surface active agent, surfactant单体 monomer和胶束 micelles状态之间的平衡 equilibrium。我们已经表明，在不同温度下进行的表面活性剂 surface active agent, surfactant溶液电导率 Conductivity测量是评估理论方法中两个关键要素——CMC和胶束 micelles电离度 degree of ionization of the micelles $\alpha$ ——的便捷途径。该实验技术代表了一种无害、简单、稳健且可重现的实验室实验，可以在本科生实验室课程中进行。对描述胶束 micelles化 micellization过程的不同热力学 Thermodynamics量的温度趋势的简单考虑，可用于进行有趣的讨论，以合理化控制溶液中这种聚集过程的基本机制。

29. 内容解释

这是文章的结论部分，对全文的工作进行了总结和评价。

• 主要贡献：本文提供了一个全新的本科实验项目，该项目能够让学生通过研究胶束 micelles体系来学习和应用基本的热力学 Thermodynamics概念。
• 理论与实践的结合：
  • 理论框架：实验数据的分析基于“闭合缔合模型 closed association model”，该模型描述了单体 monomer与胶束 micelles之间的平衡 equilibrium。
  • 实验方法：采用简单的电导率 Conductivity测量法，在不同温度下方便地测定出模型所需的两个核心参数：CMC和 $\alpha$。
• 实验的优点：
  • 无害 (harmless)：实验过程安全风险低。
  • 简单 (simple)：操作和设备要求不高。
  • 稳健 (robust)：实验结果可靠，不易受微小扰动影响。
  • 可重现 (reproducible)：不同人或不同次重复实验能得到相似的结果。 这些优点使得该实验非常适合在教学实验室中推广。
• 教学价值：
  • 本实验不仅仅是让学生练习操作和测量，更重要的是，通过分析最终得到的热力学 Thermodynamics参数（$\Delta G, \Delta H, \Delta S$）随温度的变化趋势，可以引导学生进行深入的物理化学 Physical Chemistry讨论。
  • 学生可以从中理解到，像胶束 micelles化 micellization这样看似简单的自聚集过程，其背后受控于熵 entropy、焓 enthalpy以及溶剂效应等多种复杂而深刻的基本机制。这有助于培养学生的科学探究能力和批判性思维。